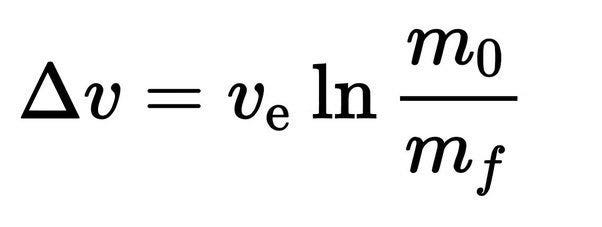Understanding Tsiolkovsky Rocket Eq.
A Layman’s Guide
The Tsiolkovsky Rocket Equation, often called the Rocket Equation, is a cornerstone of rocket science. Named after the Russian scientist Konstantin Tsiolkovsky, who derived it in 1903, this equation explains how rockets achieve the immense speeds needed to escape Earth’s gravity.
It’s an elegant formula, and while it may seem intimidating at first, we’ll break it down in simple terms with examples and illustrations to make it easy to understand.
Why Do We Need the Rocket Equation?
Rockets work by throwing stuff (fuel exhaust) out the back at high speed, which pushes them forward. This principle is called Newton’s Third Law of Motion: “For every action, there is an equal and opposite reaction.”
The Rocket Equation helps us answer a key question:
How fast can a rocket go, given a certain amount of fuel and payload?
To explore this, let’s first look at what the equation tells us.
The Rocket Equation: The Formula
The Tsiolkovsky Rocket Equation is:
Here:
Δv is the rocket’s final velocity (how fast it’s going).
vᴇ is the exhaust velocity (how fast the fuel is expelled).
ln is the natural logarithm (a mathematical function).
m₀ is the rocket’s initial mass (rocket + fuel + payload).
mf is the rocket’s final mass (rocket + payload, after fuel is burned).
At its core, the Rocket Equation tells us that the rocket’s speed depends on two things:
How fast the fuel is ejected (vᴇ). Faster exhaust means more thrust.
How much mass is lost (fuel burned). The bigger the ratio , the faster the rocket can go.
Breaking It Down for Everyday Understanding
Imagine you’re on a skateboard, holding a pile of tennis balls. If you throw one tennis ball backward, the skateboard moves forward a little. Throw more tennis balls, and you’ll move faster. If you throw them harder, you’ll move even faster.
This is essentially how rockets work:
The skateboard is the rocket.
You and the tennis balls represent the rocket with its fuel.
Throwing tennis balls is ejecting fuel at high speed.
The Rocket Equation tells us how the speed of the skateboard (rocket) changes as you throw the tennis balls (burn fuel).
Key Insights from the Equation
Exhaust Velocity Matters: The faster you can throw the tennis balls (or eject fuel), the faster you’ll move. This is why engineers design engines to eject fuel at incredibly high speeds.
Mass Ratio is Crucial: The more tennis balls you have to throw (fuel), compared to your weight and the skateboard’s weight (payload), the faster you can go. Rockets need a lot of fuel because they’re heavy, and escaping Earth’s gravity requires tremendous speed (about 11.2 km/s).
Diminishing Returns: Each additional bit of fuel adds less speed than the one before it. This is because of the logarithm in the equation. It’s why rockets are designed in stages, shedding empty fuel tanks as they go to stay as light as possible.
Example: A Simple Rocket
Let’s apply the Rocket Equation to a small hypothetical rocket:
Scenario:
Initial mass (m0): 10,000 kg (rocket + fuel + payload).
Final mass (mf): 2,000 kg (rocket + payload after fuel is burned).
Exhaust velocity (vᴇ): 3,000 m/s.
Step-by-Step Calculation:
Calculate the mass ratio
Take the natural logarithm of the mass ratio
Multiply by the exhaust velocity
So, the rocket’s final velocity is approximately 4,830 m/s. This is enough to reach low Earth orbit but not escape Earth’s gravity entirely. To go faster, we’d need more fuel or a higher exhaust velocity.
Challenges and Limitations
While the Rocket Equation is powerful, it has limitations:
Gravity and Air Resistance: The equation assumes the rocket is in space, where there’s no air resistance or gravity. Real rockets must overcome these forces during launch, requiring even more fuel.
Exponential Fuel Needs: As the rocket’s speed increases, the fuel required grows exponentially. This is why launching rockets is so challenging and expensive.
Engineering Constraints: Rockets can only carry so much fuel before their structure becomes too heavy to lift. Engineers must carefully balance fuel, payload, and efficiency.
Real-Life Applications
1. SpaceX’s Falcon 9
SpaceX’s Falcon 9 rocket uses the Rocket Equation to calculate the optimal amount of fuel needed to carry satellites into orbit. By reusing first stages, they save fuel and reduce costs.
2. Apollo Missions
The Saturn V rocket that carried astronauts to the Moon relied on the Rocket Equation to calculate the massive amount of fuel needed to escape Earth’s gravity and reach lunar orbit.
3. Mars Missions
Future missions to Mars will need advanced engines (like nuclear or ion propulsion) with high exhaust velocities to achieve the speeds required for interplanetary travel.
Why the Rocket Equation Matters
The Tsiolkovsky Rocket Equation isn’t just about numbers; it’s about understanding the physics that make space travel possible. It teaches us:
The challenges of overcoming Earth’s gravity.
The importance of efficiency in fuel and design.
How to innovate for the future of space exploration.
As humanity ventures farther into space, from the Moon to Mars and beyond, the principles behind this equation will continue to guide rocket scientists and engineers.
The Tsiolkovsky Rocket Equation may seem like a complex formula, but at its heart, it’s a simple and powerful tool that explains how rockets achieve the speeds needed to explore the cosmos. By understanding the interplay between fuel, mass, and velocity, we gain insight into the incredible feats of engineering that make space travel possible. Whether you’re a space enthusiast or just curious about how rockets work, this equation is a window into the science that propels us to the stars.